Il 29 febbraio, l’attimo fuggente
Credo che a molti sia capitato di notare che spesso, se non addirittura sempre, nelle pubblicazioni di carattere scientifico in cui lo studio trattato si corredi con tabelle annuali di valori quotidiani medii (di qualunque natura essi siano, dalle declinazioni solari alle precipitazioni pluviali, dal traffico sulle strade alla frequenza delle nascite ecc.), si riportino mese per mese tutti i giorni dal 1° al 30 o al 31, ma fermandosi per febbraio sempre e solo al 28, come se il 29 non dovesse o non potesse essere preso in considerazione, come se non esistesse… mai!
| GEN | FEB | MAR | … | |
| … | … | … | … | … |
| 27 | –18.43° | –8.30° | +2.74° | … |
| 28 | –18.16° | –7.92° | +3.13° | … |
| 29 | –17.90° | ? | +3.52° | … |
| 30 | –17.63° | +3.91° | … | |
| 31 | –17.35° | +4.30° | … |
Questa strana ed ingiustificata consuetudine d’ignorare la presenza del 29 febbraio nel calendario delle date, privandolo della sua “dignità”, è legata al concetto ed al significato di anno medio.
Sappiamo tutti come l’anno civile che definisce il proprio ciclo (il calendario) come insieme di 365 o 366 unità intere di tempo, i giorni, proprio per questa sua struttura artificiale debba fare i salti mortali per stare al passo con l’anno tropico che invece segue un proprio ritmo, naturale, senza curarsi di doverlo far corrispondere ad altre unità di tempo secondo rapporti definiti.
Senza ripetere cose già scritte altrove e note a tutti, ci basti ricordare che il calendario gregoriano attualmente in uso alterna anni civili di 365 e 366 giorni interi (a. comuni e bisestili, rispettivamente), col risultato di definire, sul ciclo completo di 400 anni, l’anno come lungo mediamente ed esattamente 365.2425d, e che l’anno tropico, dal canto suo, dura attualmente ed all’incirca 365.2422d.
Nel tabulare i valori quotidiani medii di certe grandezze come la declinazione solare, calcolati mediando gli effettivi valori assunti dalle stesse attraverso un certo numero di anni, noi non facciamo altro che dire che ad una certa data dell’anno tipo quella grandezza ha quel valore, valore medio: tutte le date dell’anno sono rappresentate, perché considerate, perché con pari “diritto”, perché con pari “peso”, durata (1 giorno) ecc. Il 29 febbraio, però, data considerata anomala, “bastarda”, quasi fastidiosa o inutile, viene regolarmente ignorata, come nell’esempio della tab. 1, qui sopra!
Per capire meglio dove voglio arrivare consideriamo prima una data comune, una data non diversa da una qualsiasi altra data dell’anno: prendiamo ad esempio il 27 febbraio. Be’, quella data torna tutti gli anni, lo sappiamo: segue il 26 febbraio e precede il 28, dura 1 giorno, il 58° dell’anno e così via. Niente di strano, tutto regolare.
Possiamo anche dire (a costo di sembrare sciocchi…) che in un anno cade una volta, o che ha il 100% di probabilità di verificarsi, come dire “è sicuro che ci sia”; che in due anni (di seguito, o qualsiasi) cade due volte (sempre 100% di probabilità, sempre data “sicura”); che in dieci anni “sicuramente” (100%) si verifica 10 volte, in 100 anni 100 volte, ed in 400 anni 400 volte…
La data seguente, anch’essa comune, si comporta allo stesso modo: il 28 febbraio c’è tutti gli anni, 10 volte in dieci anni, 200 volte in 200 anni, 400 volte in 400 anni… 100% di probabilità di verificarsi in un anno qualsiasi. Sempre. Normale.
Ma veniamo alla data successiva: il 29 febbraio. A causa dell’artificialità del contesto a cui appartiene, e della particolarità del sistema che ne regola l’esistenza, sappiamo bene che non è sicuro che la troviamo tutti gli anni, anzi il contrario: è più probabile che non ci sia il 29 febbraio in un anno qualsiasi anziché esserci.
Verificandosi un solo anno su quattro (anzi, meno), possiamo dire che la probabilità che non ci sia è del 75% o poco più, contro un 25% scarso che ci sia.
Ad essere precisi, il 29 febbraio in media, considerando il ciclo completo di 400 anni che ne regola l’inclusione nel calendario, si verifica solo 97 volte su 400, vale a dire con una frequenza solamente del 24.25%. Nessuna sorpresa, comunque.
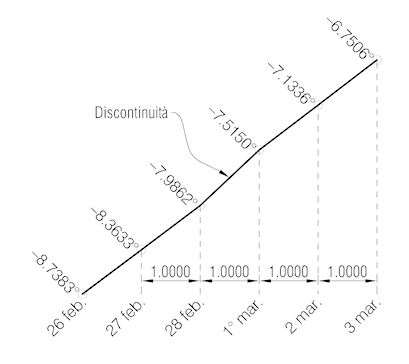
Ma proviamo ora a graficizzare i valori di una funzione con sviluppo regolare come la declinazione solare, valori medii calcolati come sopra (nel periodo 2001–2400) e presi da una tabella.
Dalla fig. 1 appare più chiaro che cosa sto dicendo: se ordino in ascissa le date, spaziandole uniformemente, ad intervalli corrispondenti esattamente ad 1 giorno intero, e riporto in ordinata i valori medii corrispondenti del fenomeno studiato, ma tra le date ignoro il 29 febbraio, rivelo in tutta evidenza una discontinuità nella curva così graficizzata della nostra funzione.
In questo caso introduco una specie d’impennata nel passaggio dal 28 febbraio al 1° marzo, che poi fortunatamente si ripiana… È evidente però che questo atteggiamento non è corretto: c’è qualcosa che non va…
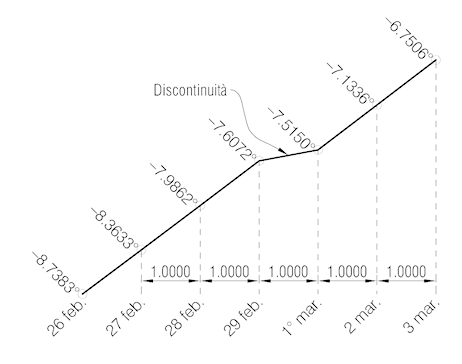
Proviamo allora a seguire un approccio differente, anzi completamente opposto: reinseriamo, come sarebbe giusto, la data del 29 febbraio tra quelle di cui graficizzare i valori, dandole lo stesso peso di tute le altre.
Se, come ho fatto nel grafico di fig. 2, reinserisco il 29 febbraio tra il 28 e il 1° marzo, dandogli però la stessa “importanza”, la stessa durata delle altre date, introduco un’altra discontinuità nello sviluppo della funzione, discontinuità contraria alla precedente, diciamo un avvallamento…
Anche in questo caso dev’esserci qualcosa che non va!
Se i due approcci appena tentati, per un verso o per un altro, danno risultati scorretti il motivo è in fondo lo stesso: il peso, l’importanza da dare alla data del 29 febbraio, o meglio la durata (dato che stiamo considerando la grandezza tempo lungo l’asse delle ascisse) non può essere né nulla (ignorandola) né unitaria (come se fosse un giorno comune), ma deve essere, per così dire, una via di mezzo tra le due.
Per queste ragioni dovrebbe essere chiaro qual è il punto…
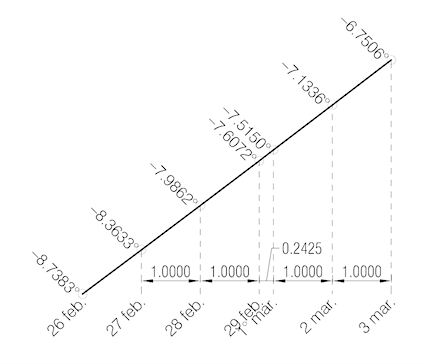
L’esatto valore da assegnare alla durata del 29 febbraio lungo l’asse delle ascisse nel grafico non è altro che quello della durata media che quella data manifesta nel periodo considerato: poiché, come dicevo all’inizio, il 29 febbraio ricorre 97 volte su 400, cioè il 24.25% delle volte, tale sarà la durata media del 29 febbraio in un grafico corretto, come appare evidente dalla fig. 3: non 0 giorni o 1 giorno, ma 0.2425 giorni.
Del resto tutte le altre date non seguono lo stesso criterio? Ciascuna ha una durata media di 1 giorno, ricorrendo il 100% delle volte, cioè tutti gli anni.
In questo modo si ristabilisce il corretto sviluppo dei valori della funzione.

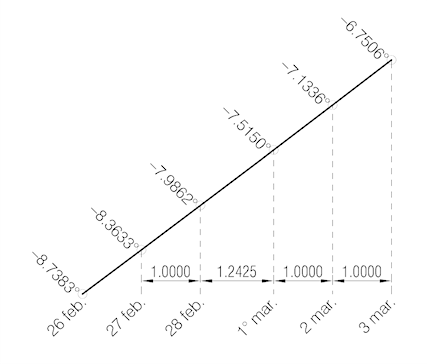
Per concludere devo dire che un risultato simile si potrebbe ottenere anche dai valori di una tabella che ignorasse il 29 febbraio (come quelle che compaiono in quasi tutte le pubblicazioni, come dicevo all’inizio, e che abbiamo usato per il grafico di fig. 1), semplicemente immaginando che il 28 febbraio durasse mediamente non 1 ma 1.2425 giorni.
Come si può vedere dal grafico nella fig. 4, l’accorgimento per dare alla curva della funzione la propria continuità è appunto quello di assegnare al 28 febbraio una durata media di 1.2425d.
Se poi da simili tabelle (o grafici) si volesse ricavare il valore medio della declinazione solare al 29 febbraio, e colmare così la lacuna, allora basterebbe compiere una semplice interpolazione, come la seguente:
$\left\{ \begin{align} & \frac{\delta --7.9862{}^\circ }{{{1}^{d}}}=\frac{-7.5150{}^\circ --7.9862{}^\circ }{{{1.2425}^{d}}} \\ & 1.2425\cdot \delta +9.9228535{}^\circ =-7.5150{}^\circ +7.9862{}^\circ \\ & 1.2425\cdot \delta =-\text{9}\text{.4516535}{}^\circ \\ & \delta \text{=}\frac{-\text{9}\text{.4516535}{}^\circ }{1.2425}=-7.6070{}^\circ \\ \end{align} \right.$
Il valore così calcolato differisce da quello “reale” di 2 decimillesimi di grado.
